2025年杭州泛函分析与量子理论研讨会是杭州地区的高水平学术盛会。本次会议旨在推动跨学科深度融合,促进该领域的学术交流与合作,提升杭州地区在该领域的学术水平,探讨前沿学术问题。 会议邀请了多位具有重要影响的专家学者莅临指导。
本次会议由浙江科技大学理学院承办,得到了理学院高峰学科基金和国家自然科学基金的支持。
会议时间: 2025年4月18日—21日
会议地点: 浙江宾馆(杭州三台山路278号)
特邀专家
(按姓名拼音首字母排序)
郭坤宇 教授 复旦大学
侯晋川 教授 太原理工大学
蒋春澜 教授 河北师范大学
李永明 教授 陕西师范大学
卢玉峰 教授 大连理工大学
徐宪民 教授 嘉兴大学
周泽华 教授 天津大学
会议组委会联系人:
叶善力:slye@zust.edu.cn
李爱军:liaijun72@163.com
陶元红:taoyuanhong12@126.com
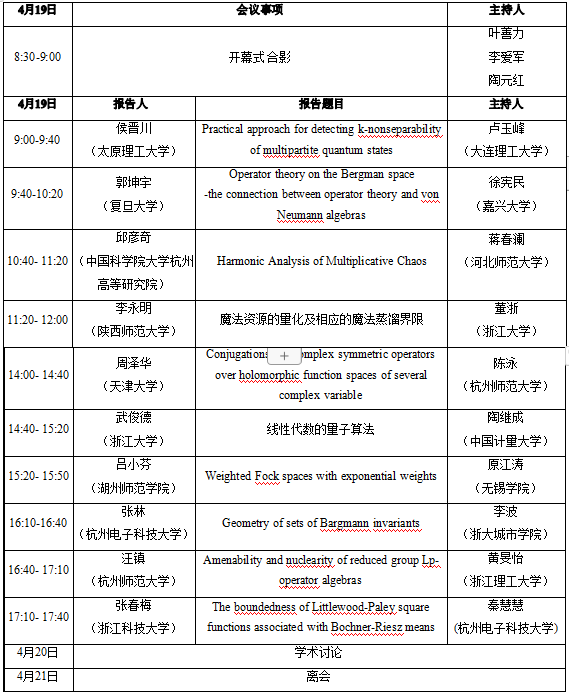
2025年杭州泛函分析与量子理论研讨会日程
报告题目及摘要
Practical approach for detecting k-nonseparability of multipartite quantum states
侯晋川
太原理工大学
The instantaneous detection of entanglement in quantum states poses a significant challenge in the fields of quantum computation and quantum information, and there are no practical methods or tools to complete this task satisfactorily so far. We propose a sufficient and necessary criterion of k-nonseparability for any n-partite finite or infinite dimensional systems, 2 ≤ k ≤ n. This criterion serves as the foundation for a practical scheme designed to detect entanglement and k-nonseparability across multipartite finite-dimensional systems. To exemplify the application of our scheme, we have developed a software tool that facilitates swift and precise identification of entanglement, k-nonseparability, and genuine entanglement within n-qubit systems, specifically tailored for systems with 2 ≤ n ≤ 4.
侯晋川,汉族,博士,太原理工大学数学学院教授,博士生导师。多年来从事数学的教学和科研工作,研究方向为算子理论、算子代数和量子信息理论。主持完成科研项目28项,其中国家级11项,省部级17项。主要从事算子代数、算子理论及在量子信息等领域中的应用研究。在国内外数学及物理杂志上发表学术论文290余篇(物理杂志发表40余篇),其中SCI收录180余篇;出版专著一部。获中国青年科技奖1项;山西省科技进步一等奖2项;山西省自然科学二等奖2项。曾获山西省优秀回国留学人员奖,国务院政府特殊津贴,山西省优秀专家,山西省第二届科技功臣,山西省劳模,山西省特级劳模,全国做出突出贡献的回国留学人员,全国优秀教师、全国五一劳动奖章,全国先进工作者。
Operator theory on the Bergman space
-the connection between operator theory and von Neumann algebras
郭坤宇
复旦大学
In this talk, we will combine methods of complex analysis, operator theory and conformal geometry to construct a class of type II factors in the theory of von Neumann algebras, which arise essentially from holomorphic coverings of bounded planar do mains. One will see how types of such von Neumann algebras are related to algebraic topology of planar domains. As a result, we established a fascinating connection to one of the long-standing problems in free group factors. An interplay of analytical, geometrical, operator and group theoretical techniques is intrinsic to this work. This work is based on the monograph “Multiplication operators on the Bergman space” by Guo and Huang.
郭坤宇,复旦大学特聘教授、上海数学中心谷超豪研究所长聘教授。长期从事泛函分析的教学和科研工作,在国际知名数学期刊发表论文100多篇: 包括 JFA(13篇)、 Crelle’s Journal(3篇)、Adv. Math. (3篇)、Math.Ann.、 Proc. LMS等; 国外出版专著2部(Lecture Notes in Math;π-Research Notes in Math.)。 发展的思想、技术和方法被学界同行称为 “郭方法”; “郭引理”;“郭-稳定性”; “郭-王定理”;“郭-王恒等式”等。 解决了算子理论中多个困难的问题,形成了复旦大学算子理论研究特色,国际同行称为 “Fudan group”。2005年获国家杰出青年科学基金、2006年被聘为教育部长江学者特聘教授。先后两次获上海市自然科学奖一等奖(均为第一完成人),上海市自然科学牡丹奖、上海市领军人才等。曾任复旦大学数学科学学院院长、非线性数学模型与方法教育部重点实验室主任。现为第十四届全国政协委员。
Harmonic Analysis of Multiplicative Chaos
邱彦奇
中国科学院大学杭州高等研究院
I will introduce a general method in dealing with Fourier decay of random measures arising from Kahane's T-martingale theory, thus including Mandelbrot Cascades (canonical or microcanonical), Gaussian Multiplicative Chaos, Random Coverings and more abstract ones. This very new method is a combination of many fundamental vector-valued martingale inequalities such as Pisier's martingale type inequality, Burkholder-Rosenthal inequality, Bourgain-Stein inequality etc and also an idea which seems to related to the decoupling method in harmonic analysis. The talk is based on joint works with Xinxin Chen, Yong Han, Zipeng Wang, and with Zhaofeng Lin, Mingjie Tan.
邱彦奇,国科大杭州高等研究院基础物理与数学科学学院研究员,国家级青年人才入选者。2007年从清华大学考入巴黎高等师范,2010年获巴黎六大数学硕士学位。2013年获得巴黎六大数学博士学位。2013至2015年在Ax-Marseile大学从事博士后研究工作。2015年通过选拔录取为法国国家科研中心(CNRS)副研究员。2017年在中科院数学所任副研究员,2019年晋升为研究员。2021年兼职武汉大学数学与统计学院教授。2023年在国科大杭州高等研究院任研究员。其研究工作涵盖泛函分析、随机分析和调和分析等分析数学多个领域,取得了一系列重要研究成果。
魔法资源的量化及相应的魔法蒸馏界限
李永明
陕西师范大学
魔法(magic)是实现量子计算所必需的资源,因此对魔法资源理论的定量研究成为一个非常重要的任务。而对魔法资源的量化又主要分为静态系统和动态系统的量化。对于静态系统,我们将定义在qubits上的稳定子Rényi熵推广到了qudits上,证明了其是一定义良好的魔法资源度量,并给出了这个度量更紧的上界。对于动态系统,我们定义了量子信道的Pauli谱的概念,并且我们给出了信道的稳定子Rényi熵以及稳定子零度的概念。此外,我们还研究了我们给出的度量与魔法蒸馏之间的关系,并证明了使用我们的度量,给出的蒸馏效率会更高。我们的结果为研究魔法资源理论和魔法蒸馏提供了新的思路和视野。
李永明,教授,博士,陕西师范大学二级教授,博士生导师。主要研究方向为非经典计算理论、量子计算与量子信息、格上拓扑学。政府特殊津贴获得者,教育部高校青年教师奖获得者,陕西省三秦人才津贴获得者。(曾)担任国际IEEE计算智能模糊系统技术委员会委员,中国系统工程学会模糊系统与模糊数学委员会副主任委员,全国运筹学会智能计算学会副理事长,全国高等师范学校计算机教育委员会副理事长,中国计算机学会理论计算机学会理事,陕西省计算机学会常务理事,CCF(中国计算机学会)西安分部执委。曾获得陕西省科学技术奖,教育部高等学校科学研究优秀成果奖自然科学奖等。
Conjugations and complex symmetric operators over holomorphic
function spaces of several complex variable
周泽华
天津大学
In this talk, we will present the following results:
1. Several class of on holomorphic function spaces of of some high-dimensional domains Omega on C^n.
2. Some sufficient and necessary conditions for Teoplitz operators to be complex symmetric with
respect to these specific conjugations.
3. Whether does there exist any other complex symmetric operator on holomorphic function spaces or not?
周泽华,教授,博士生导师。曾任天津大学数学系主任,三个数学杂志编委。2005-1017年任教育部大学数学课程教学指导委员会委员,多次参加国家自然科学基金优青,以及重点项目的会评。国家级《数学与应用数学》特色专业建设负责人,国家级《数学分析》一流课程建设负责人。现任天津市数学会常务理事。研究方向:多复变与复几何;函数空间与算子理论; 线性动力系统。早期涉及多复变的值分布与dbar方程的研究。近年来,主要从事多复变函数空间与算子理论及线性动力系统等方面的研究。作为项目负责人承担国家自然科学基金项目7项,发表论文150多篇。主要结果发表在《Sbornik Mathematics(苏联科学院数学)》《Math. Z》《Michigan Math. J.》《J. Operator Theory》《Indiana Univ. Math. J.》《Illinois J. Math.》《C. R. Math. Acad. Sci. Paris》《Internat. J. Math.》《Proc. Amer. Math. Soc.》《中国科学》等国际数学期刊上。
线性代数的量子算法
武俊德
浙江大学
在这个报告中,我将介绍线性代数一些基本运算的量子算法,包括向量的内积、矩阵的加法、矩阵的乘法、矩阵的逆、矩阵的行列式、矩阵的伴随矩阵、解线性方程组、矩阵的奇异值、奇异向量、矩阵的广义逆、以及某些量子态的制备等。其基本思路是借助于多量子比特Toffoli-门和1-量子比特门,并应用辅助测量去掉所有运算垃圾。通过控制量子测量技术,提高了运算成功概率。所有算法都给出了线路构造,为量子计算的集成化提供了基础。
武俊德,浙江大学数学学院教授,主要研究方向为泛函分析、量子信息与量子计算,是国内最早开展量子信息与量子计算研究和教学的数学工作者之一,在物理评论快报、数学物理杂志、物理评论(A)、物理杂志(A)、物理快报(A)等刊物发表多篇量子信息与量子计算方面的研究论文。
Weighted Fock spaces with exponential weights
吕小芬
湖州师范学院
In this talk, we introduce a kind of weighted Fock space F_φ^p on the complex plane ∁, and obtain some estimates on the Bergman kernel function. As an application, we discuss the Bergman projection, density and L_φ^p-regularity of the canonical solution to ∂ ̅.
吕小芬,湖州师范学院教授。长期从事函数空间与算子理论研究,在中国科学、J. Funct. Anal.、Integral Equ. Oper. Theory等国内外学术期刊发表论文30余篇,其中SCI收录20余篇;入选浙江省高校领军人才培养计划高层次拔尖人才、“南太湖本土高层次人才特殊支持计划”自然科学、工程技术领域青年拔尖人才、湖州市“1112”人才工程培养人选,获2021年度湖州市青年科技英才荣誉称号。
Geometry of sets of Bargmann invariants
张林
杭州电子科技大学
Certain unitary-invariants, known as Bargmann invariants or multivariate traces of quantum states, have recently gained attention due to their applications in quantum information theory. However, determining the boundaries of sets of Bargmann invariants remains a theoretical challenge. In this study, we address the problem by developing a unified, dimension-independent formulation that characterizes the sets of the 3rd and 4th Bargmann invariants. In particular, our result for the set of 4th Bargmann invariants confirms the conjecture given in [Fernandes \emph{et al.}, \href{https://doi.org/10.1103/PhysRevLett.133.190201}{\textbf{133}, 190201 (2024)}]. Based on the obtained results and numerical evidence, we conjecture that the unified, dimension-independent formulation of the boundaries for sets of 3rd-order and 4th-order Bargmann invariants may extend to the general case of the $n$th-order Bargmann invariants. Regarding this conjecture, we offer a qualitative, albeit mathematically non-rigorous, explanation of the proof. These results deepen our understanding of the fundamental physical limits within quantum mechanics and pave the way for novel applications of Bargmann invariants in quantum information processing and related fields.
张林,杭州电子科技大学理学院教授,2012年获得浙江大学博士学位,曾在德国马普所访问一年开展合作研究。主要研究领域为量子信息理论,研究兴趣包括量子信息中的随机矩阵方法、熵不等式;李群表示论在量子信息中的应用;几何不变理论在量子信息中的应用等。在数学物理和量子信息领域重要期刊:Physical Review A、Physical Review E、Annalen der Physik、Annals of Physics、Journal of Physics A: Mathematical and Theoretical等上发表论文40余篇。
Amenability and nuclearity of reduced group Lp-operator algebras
汪镇
杭州师范大学
Let p>1 and let G be a discrete group. G. An, J.-J. Lee, and Z.-J. Ruan introduced p-nuclearity for Lp-operator algebras. They proved that the reduced group Lp-operator algebra is p-nuclear if the group is amenable. In this paper, we show that the converse holds, resolving an open problem posed by N. C. Phillips concerning the p-nuclearity for reduced group Lp-operator algebras.
汪镇,杭州师范大学副教授。2018年博士毕业于华东师范大学数学科学学院,2022年3月-2024年3月在吉林大学做博士后。主持国家自然科学基金青年项目、中国博士后基金面上项目。主要从事Lp-算子代数的研究,相关成果发表于Israel J. Math.、Math. Z.等杂志。
The Boundedness of Littlewood-Paley Square Functions Associated
with Bochner-Riesz means
张春梅
浙江科技大学
In this talk, we will investigate the boundedness and compactness of the commutator of Stein’s square function, introduce the area integrals and functions associated to Bochner-Riesz means and discuss their weak type endpoint estimates and strong (p,p) boundedness for 1< p <∞ on the space of homogeneous type.
张春梅,2023年博士毕业于北京师范大学,毕业后就职于浙江科技大学。主要研究方向是调和分析及其应用,已在博士J. Geom. Anal.、Collect. Math.等SCI期刊上发表学术论文多篇。